



Next: Implementation
Up: Joyal bounds
Previous: Joyal bounds
Contents
Let a polynomial whose interval coefficients have a fixed sign. Let 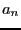 be
the leading coefficient such that
be
the leading coefficient such that 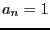 . We define the sequence
. We define the sequence
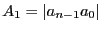 ,
,
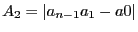 ,
,
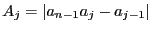 . If
. If 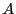 is the largest upper bound of the
sequence
is the largest upper bound of the
sequence 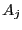 , then the modulus
, then the modulus 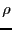 of the roots of the polynomial
is lower or equal to
of the roots of the polynomial
is lower or equal to
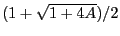 .
.
Jean-Pierre Merlet
2012-12-20