



Next: Example
Up: Laguerre method
Previous: Mathematical background
Contents
This procedure is able to give upper and lower bound on the value of
the roots.
In the implementation we define 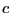 as the smallest real which satisfy
as the smallest real which satisfy
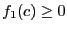 . If we find
. If we find 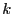 such that
such that 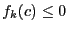 , then we
increase
, then we
increase 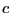 by a given positive value sens and start again. We
limit the number of iteration of the scheme by giving a maximal value
for the number of iteration:
by a given positive value sens and start again. We
limit the number of iteration of the scheme by giving a maximal value
for the number of iteration:
int Laguerre_Bound_Interval(int Degree,VECTOR &Coeff,double sens,int MaxIter,double *bound);
with:
- Degree: degree of the polynomial
- Coeff: the Degree+1 coefficients of the
polynomial in increasing degree
- sens: a positive real indicating the increase of
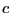 in the
scheme
in the
scheme
- MaxIter: the maximum number of iteration. If this number
is exceeded the procedure returns 0.
- bound: the upper value of the real root
This procedure fail and returns 0 if Degree=0,
Coeff(1)=0, if Coeff(Degree+1)=0 and if the number of
iteration exceed MaxIter.
On success the return code is 1. Note that the bound given by Laguerre
(assuming that Coeff(Degree+1) is positive) cannot be lower
than -Coeff(Degree)/Coeff(Degree+1).
The lower bound of the root may be determined by:
int Laguerre_Bound_Inverse_Interval(int Degree,VECTOR &Coeff1,double amp_sens,
int MaxIter,double *bound);
We have also a procedure which determine upper and lower bound for the
real roots:
int Laguerre_Bound_Interval(int Degree,VECTOR &Coeff,double sens,int MaxIter,INTERVAL &Bound);
All the real roots lie within Bound. We may also use this
procedure for interval polynomial:
int Laguerre_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,double sens,
int MaxIter,INTERVAL &Bound);
This procedure fail and returns 0 if Degree=0,
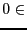 Coeff(1), if
Coeff(1), if 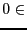 Coeff(Degree+1)
and if the number of
iteration exceed MaxIter.
If Bound=[a,b], then the real roots of all the polynomial in the
set are lower than b and for some polynomial in the set the roots may
be lower than a. A similar procedure exists for upper and lower bound.
Coeff(Degree+1)
and if the number of
iteration exceed MaxIter.
If Bound=[a,b], then the real roots of all the polynomial in the
set are lower than b and for some polynomial in the set the roots may
be lower than a. A similar procedure exists for upper and lower bound.
int Laguerre_Bound_Interval(int Degree,INTERVAL_VECTOR &Coeff,double sens,
int MaxIter,INTERVAL &Lower,INTERVAL &Upper);
In that case Upper=[a,b] will be such that
value of all roots of any
polynomial within the set is lower than b, while for some polynomial
they will be lower than a. On the other hand Lower=[a,b]
will be such that the
value of all roots of any
polynomial within the set is greater than a, while for some polynomial
they will be greater than b.




Next: Example
Up: Laguerre method
Previous: Mathematical background
Contents
Jean-Pierre Merlet
2012-12-20