Implementation

Rouche theorem is implemented in the following way:

• Rouche theorem is checked with respect to the mid-point of a box
• if Roucche theorem is satisfied, then a limited number of Newton iteration is performed to check if Newton indeed converge. If this is the case a ball that include a single solution has been determined
• if a ball has been determined, then, optionaly an inflation procedure )see section 3.1.6) is used to try to enlarge the ball

The syntax of the procedure is:

 
int Rouche(int DimensionEq,int DimVar,int order,
           INTERVAL_VECTOR (* TheIntervalFunction)(int,int,INTERVAL_VECTOR &),
           INTERVAL_VECTOR (* Jacobian)(int, int, INTERVAL_VECTOR &), 
           INTERVAL_MATRIX (* Gradient)(int, int, INTERVAL_VECTOR &), 
           INTERVAL_VECTOR (* OtherDerivatives)(int, int, INTERVAL_VECTOR &), 
           double Accuracy,
           int MaxIter,
           INTERVAL_VECTOR &Input,
           INTERVAL_VECTOR &UnicityBox)

where

• DimensionEq: number of equations
• DimVar: number of variables
• order: the order for Rouche theorem minus 1
• TheIntervalFunction: a procedure in MakeF format for computing an interval evaluation of the equations
• Jacobian: a procedure in MakeF format that computes the jacobian row by row
• Gradient: a procedure that compute the jacobian in MakeJ format
• OtherDerivatives: a procedure in MakeF format that computes the derivative of order larger or equal to 2, row by row. This procedure returns an interval vector of dimension ${\tt order}{\tt DimensionEq}^2$

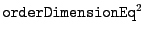
The parameters Accuracy is used in the Newton scheme to determine if Newton has converged i.e. if the residues are lower than Accuracy. A maximum of MaxIter iterations are performed. The solution found with Newton is stored in ALIAS_Simp_Sol_Newton_Numerique while a copy of the unicity box is available in ALIAS_Simp_Sol_Newton

If a ball with a single solution has been found it will be returned in UnicityBox and the procedure returns 1, otherwise it returns 0.

If the flag ALIAS_Always_Use_Inflation is set to 1, then an inflation procedure is used to try to enlarge the box up to the accuracy ALIAS_Eps_Inflation.