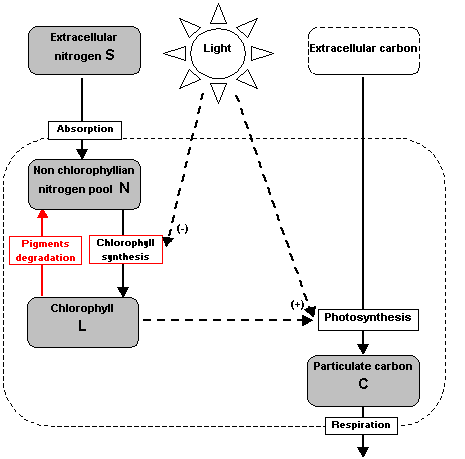
Conceptual schema of the model
Modelling phytoplankton growth in chemostat
Lionel Pawlowski
Olivier Bernard
Antoine Sciandra
1. Introduction.
2. Biological adaptations of phytoplankton to light and nitrate limitations.
3. Experimental facts.
4. Model overview.
5. Qualitative steady input-output behaviour.
6. Parameters Identification.
7. Dynamic simulations.
8. Bibliographic notes.
The estimation of the amount of CO2 fixed by oceanic phytoplankton during primary production is a key point to quantify the future evolution of atmospheric carbon. Modelling of phytoplankton growth is therefore an important challenge to improve the predictions on planet global warming. Light, nutrients and temperature are generally considered as the main factors affecting phytoplankton growth (Chalup and Laws, 1990). In stratified waters, light is available in the surface layer but nitrates are generally present at low concentrations. On the contrary, in the deep layer, light is low and nitrate abundant. For intermediate situations, light and nitrates are both at suboptimal levels for phytoplankton growth. Moreover, due to vertical mixing, cells are continuously exposed to a variable environment, and must adapt their metabolism to sustain an optimal growth under opposing gradients of light and nitrogen. We propose a model that will describe the phytoplanktonic behaviour when both nitrogen and light are at suboptimal level.
2. Biological adaptations of phytoplankton to light and nitrate limitations
Experimental studies (Rhee and Gotham, 1981) have highlighted the interaction between light and nutrients on growth through a physiological adaptation known as the compensation phenomenon. The cell can compensate a decrease of light intensity by optimising its ability to harvest photons through an increase of its pigment content (Falkowski and Owen, 1980) and by regulating the Ribulose-1,5-bisphosphate carboxylase/oxygenase (Rubisco). Rubisco and chlorophyll represent large nitrogen reserves in the cell and vary with the nitrogen status and light limitation (Sciandra et al., 1997). For a decreasing irradiance, the cell requires more nitrogen (chlorophyll per cell, protein and RNA increase) so this adaptation is only possible when nitrogen concentration in the water is sufficient to respond to the cell requirements. These changes in the cell content may be assessed by measurements of nitrogen, chlorophyll and carbon. Common descriptors are the chlorophyll to carbon (Chla:C) and nitrogen to carbon ratios (N:C). The Chla:C ratio is commonly used as an indicator of the physiological acclimatation of the cell. This ratio has been often used as a state variable in many growth models (see for example Zonneveld, 1998) as it allows one to convert chlorophyll a measurements in carbon data. The N:C ratio is an indicator of the accumulation and the mobilisation of energy reserves in the cell (Geider et al., 1998). Both ratios decrease with light for a given dilution rate (Chalup and Laws, 1990).
The following biological features have been observed experimentally:
Carbon concentration increases with light and decreases with dilution rate d (see Geider et al.,1998).
Chlorophyll concentration is a decreasing function of the light due to photoadaptation (Laws and Bannister, 1980). It increases with the dilution rate.
Chl:C increases with the dilution rate and decreases with light intensity (Chalup and Laws, 1990; Geider et al., 1998; Falkowski, 1997).
N:C increases with the dilution rate (Chalup and Laws, 1990) and decreases with light.
Many phytoplankton growth models have been developed for one limiting factor such as nutrient, light or temperature. Models integrating more than one limitation are often difficult to validate for two reasons. First, they often use numerous parameters that are difficult to identify from the available data (e.g. Geider et al.,1998). Secondly, as they tend to describe detailed cellular processes, state variables often represent quantities that can not be measured experimentally (e.g. Shuter, 1979). Our model integrates both limitations by light and nitrogen. It has been designed to have a simple formulation with few parameters. Three of the four state variables represent measurable quantities in a photobioreactor or in the open sea (chlorophyll, carbon, nitrate, particulate nitrogen). These features permit easier identification and validation.

Conceptual
schema of the model
|
|
where |
|
Model formulation
|
Parameters |
Symbols |
|
Maximum uptake rate |
|
|
Half saturation constant for nitrate absorption |
ks |
|
Maximum chlorophyll synthesis rate |
kl |
|
Threshold coefficient for chlorophyll synthesis |
kc |
|
Maximum carbon fixation rate |
|
|
Half saturation constant for carbon fixation |
ki |
|
Pigment degradation rate |
|
|
Respiration rate |
|
Table of parameters
5. Qualitative steady input-output behaviour
The analysis of the qualitative properties allows a structural validation of the model, independently from the parameter values. The aim of this analysis is to determine whether the steady input-output properties of the model are consistent with the observations. Steady-state outputs are deduced by resolving the system dS(t)/dt=0, dN(t)/dt=0, dL(t)/dt=0, dC(t)/dt=0 and are compared to their experimental equivalent. Relationships are expressed as functions of i (light term) and D (dilution rate). Comparisons with experimental data show that the proposed model has the same observed steady input-output behaviour.
|
|
Quantity |
Light i |
Dilution rate D |
||
|
Carbone C* |
+ |
+ |
|||
|
Chlorophyll L* |
- |
+ |
|||
|
Non chlorophyllian nitrogen N* |
+ |
- |
|||
|
N*:C* |
- |
+ |
|||
|
L*:C* |
- & + |
+ |
|||
Steady-state
solutions and qualitative input-output behaviour of the model
(+:
increasing, -: decreasing, - & +: decreasing then increasing).
|
|
|
Steady-state
concentrations for particulate carbon (a) and chlorophyll a (b) at
different dilution rates.
Solutions evolves accordingly to
observations.
Steady input-output behaviour is used in order to identify the model parameters. The proposed approach allows to decouple the parameter estimations (they are identified by small sets) and provides at the same time a way to validate the model. For sake of conciseness, we will explain the idea of the method with an example based on the steady input-output behaviour obtained for the ratio L*:C*:
![]()
This
expression can be seen as a linear relationship between the steady
ratio L*:C* and the combinations of inputs given by D/I, D
and I. Therefore, there is a regression between these known
quantities and the unknown ratios originating from the combination of
the model parameters ki,
![]() ,
,![]() ,
,![]() .
In theory, a least square minimization of this regression for more
than 4 independent data sets will provide an estimate of these
unknown ratios. Nevertheless this method involves many unknowns in
the regression, and therefore we propose to improve it as follows. We
will consider equation L*:C* obtained for 2 different values
of i, denoted i1 and i2.
The difference between the values of L*:C* obtained for the
same dilution rate D is given by:
.
In theory, a least square minimization of this regression for more
than 4 independent data sets will provide an estimate of these
unknown ratios. Nevertheless this method involves many unknowns in
the regression, and therefore we propose to improve it as follows. We
will consider equation L*:C* obtained for 2 different values
of i, denoted i1 and i2.
The difference between the values of L*:C* obtained for the
same dilution rate D is given by:
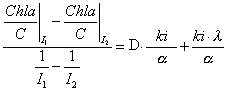
The new
relation is expressed as a linear function of D. A simple
linear regression using experimental data will then provide an
estimate of
![]() .
The significance of the regression with respect to the data may be
statistically checked to assess the quantitative validity of the
steady input-output behaviour.
.
The significance of the regression with respect to the data may be
statistically checked to assess the quantitative validity of the
steady input-output behaviour.
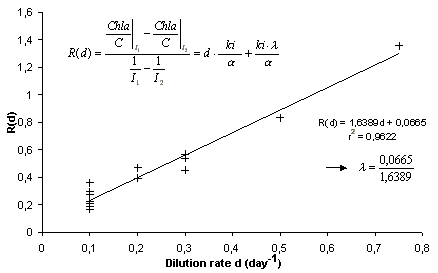
Identification
of the parameter
![]() with a linear regression.
with a linear regression.
Of course,
![]() and ki can not be directly evaluated from this regression,
but from other relationships. Except
and ki can not be directly evaluated from this regression,
but from other relationships. Except
![]() m
and ks, all parameters have been identified with this
method.
m
and ks, all parameters have been identified with this
method.
![]() m
and ks are identified in batch conditions (dilution rate is
zero) at the beginning of each experiments since the kinetic nitrates
absorption is adequately estimated only when the nitrate
concentration is detectable (after it falls under the detection
threshold). Only after this step of steady-state identification,
parameters tuning is improved by a global least square minimization,
starting with initial parameter values provided by the previous
approach. The resulting values of the parameters do not differ
greatly from the values obtained by the exploitation of the steady
input-output behaviour.
m
and ks are identified in batch conditions (dilution rate is
zero) at the beginning of each experiments since the kinetic nitrates
absorption is adequately estimated only when the nitrate
concentration is detectable (after it falls under the detection
threshold). Only after this step of steady-state identification,
parameters tuning is improved by a global least square minimization,
starting with initial parameter values provided by the previous
approach. The resulting values of the parameters do not differ
greatly from the values obtained by the exploitation of the steady
input-output behaviour.
|
Symbols |
Values |
Units |
|
|
0.5 |
µmol N.µmol C-1.d-1 |
|
ks |
0.43 |
µM N |
|
kl |
6.59 |
n.d. |
|
kc |
33.0 |
µmol quanta.m-2.s-1 |
|
|
24.1 |
d-1 |
|
ki |
208.5 |
µmol quanta.m-2.s-1 |
|
|
0.054 |
d-1 |
|
|
0.345 |
d-1 |
Estimates of the model parameters.
Dynamic simulations are compared to experimental time series. The model is integrated with a second order Runge-Kutta method with variable step time. Three criteria are used to evaluate the model:
1) the difference between steady observations and model predictions.
2) the ability to describe transient phases obtained between two steady-states when the dilution rate has been modified.
3) the ability to describe batch mode results.
Chlorophyll and carbon predictions are close to experiments for steady-state conditions but in some extreme cases of very low or high dilution or light intensities, the output of chlorophyll and carbon may be under- or overestimated. Transient phases are evolving accordingly to the experimental data. Carbon predictions are particularly close to measurements. For Chlorophyll, the model reproduces less precisely measurements.
Although this model is made of simple assumptions and has few parameters, it reproduces correctly the qualitative and quantitative input-output behaviour observed in the experiments. More generally, we have demonstrated in this approach the utility of the steady input-output behaviour in order to validate and calibrate a biological model which is often made of speculative hypotheses.
|
|
|
Steady-state
concentrations for particulate carbon and chlorophyll a at different
dilution rates.
Solutions evolves accordingly to observations.
Bannister
TT, 1979. Quantitative description of steady state,
nutrient-saturated algal growth including photoadaptation. Limnol.
Oceanogr., 24(1): 76-96.
Chalup M.S., Laws E.A., 1990.
A test of the assumptions and predictions of recent microalgal growth
models with the marine phytoplankter Pavlova lutheri. Limnol.
Oceanogr., 35(3): 583-596.
Falkowski P.G., Owens
T.G., 1980. Light-shade adaptation: two strategies in marine
phytoplankton. Plant Physiol., 66: 592-595.
Geider
R.J., MacIntyre H.L., Kana T.M., 1998. A dynamic regulatory
model of phytoplanktonic acclimatation to light , nutrients and
temperature. Limnol. Oceanogr., 43(4): 679-694.
Laws
E.A., Bannister, 1980. Nutrient- and light-limited growth of
Thalassiosira fluviatilis in continuous culture with implications for
phytoplankton growth in the ocean. Limnol. Oceanogr., 25(3):
457-473.
Rhee G.Y., Gotham I.J., 1981. The
effect of environmental factors on phytoplankton growth : light and
the interactions of light with nitrate limitation. Limnol.
Oceanogr., 26(4): 649-659.
Sciandra A., Gostan
J., Collos Y., Descola-Gros C., Leboulanger C., Martin-Jézéquel
V., Denis M., Lefèvre D., Copin-Montégut C., Avril B.,
1997. Growth-compensating phenomena in continuous cultures
of Dunaliella tertiolecta limited simultaneously by light and
nitrate. Limnol. Oceanogr., 42(6): 1325-1339.
Shuter,
B., 1979. A model of physiological adaptation in unicellular
algae. J. Theor. Biol., 78: 519-552.
Zonneveld
C., 1998. A cell-based model for the chlorophyll a to carbon
ratio in phytoplankton. Ecol. Modelling, 113(1-3): 55-70.