


Next: About this document ...
Symbolic Analysis Workshop @ FoCM, Hong Kong
http://www-sop.inria.fr/cafe/SA08
Date: June 24-26, 2008
| |
Tuesday 24th |
Wednesday 25th |
Thursday 26th |
| |
|
|
|
| 13:50-13:30 |
Moulay Barkatou |
Min Wu |
Markus Rosenkranz |
| 14:40-15:20 |
Peter van der Kamp |
George Labahn |
Elizabeth Mansfield |
| |
|
|
|
| 15:30-16:00 |
coffee break |
coffee break |
coffee break |
| |
|
|
|
| 16:00-16:40 |
Peter Paule |
José Cano |
Peter Olver |
| 16:50-17:30 |
Raimundas Vidunas |
Ekaterina Shemyakova |
Hiroshi Umemura |
| 17:40-18:20 |
Xiao-Shan Gao |
Mark Hickman |
Ziming Li |
Hypergeometric Solutions of Systems of
Linear Difference Equations and Applications
M. A. Barkatou
XLIM Institute,
Université de Limoges,
France
moulay.barkatou@xlim.fr
In this talk we present a new algorithm for computing hypergeometric
solutions of systems of linear difference equations and discuss
applications to finding 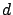 'th order (
'th order (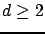 ) right-hand
factors of a given linear difference operator with polynomial coefficients.
) right-hand
factors of a given linear difference operator with polynomial coefficients.
This talk is based on a joint work with Mark van Hoeij.
Formal power series solutions of Ordinary Differential Equations and
the Newton polygon method.
Jose Cano
Departemento Algebra, Geometría y Topología,
Universidad de Valladolid, Spain.
jcano@agt.uva.es
The Newton polygon method has proved useful for finding
power series (with real exponents) solutions of differential equations.
The method is an extension by Briot and Bouquet (1856) and
Fine (1889) of the polygon construction used by
Puiseux in his studies of algebraic curves.
Despite its elementary nature, it has been used for proving
some remarkable results we shall review, with special emphasis
in a recent one: that the set of truncations of generalized power
series solutions of an ODE is contained in a semi-algebraic
set whose dimension is bounded by two times the order
of the equation.
Characteristic Set Method for Differential-Difference Polynomial
Systems
Xiao-Shan Gao
Key Laboratory of Mathematics Mechanization,
AMSS,
Chinese Academy of Sciences, Beijing, China
xgao@mmrc.iss.ac.cn
In this talk, we present a characteristic set method for
mixed differential and difference polynomial systems. We will
introduce the concepts of coherent, regular, proper irreducible, and
strongly irreducible ascending chains and their properties. We give
an algorithm which can be used to decompose the zero set for a
finitely generated differential and difference polynomial set into
the union of the zero sets of regular and consistent ascending
chains. As a consequence, we give an algorithm to solve the perfect
ideal membership problem for differential and difference
polynomials.
EXTERIOR – a MAPLE 10/11 library for computations in exterior calculus
Mark Hickman
Department of Mathematics & Statistics
University of Canterbury, New Zealand
M.Hickman@math.canterbury.ac.nz
EXTERIOR is a package for MAPLE 10/11 that implements the exterior calculus. It al-
lows the construction of jet bundles and exterior differential systems. The user interface is
designed to mimic (as much as possible) standard mathematical notation both for the user
input and the output. The package allows the user to compute, for example, symmetries
of partial differential equations and exterior differential systems, characteristic vectors,
Maurer-Cartan forms, torsion of lifted coframes and invariants that arise in the Cartan
method of equivalence.
This talk will give concrete examples of computations using this package. In addition
a discussion of the MAPLE code will be given.
Symmetries of PDEs, and integrability
Peter van der Kamp
Mathematics, La Trobe University, Victoria, Australia.
peterhvanderkamp@gmail.com
In the majority of cases where exact solutions of differential
equations can be found, the underlying property is a (continuous)
symmetry of the equation. And, in the theory of integrable
equations, the recognition and classification methods based on the
existence of symmetries have been particular successful.
A symmetry-group transforms one solution of an equation to another
solution of the same equation. This idea goes back to Sophus Lie.
Olver writes: The great power of Lie group theory lies
in the crucial observation that one can replace the complicated,
nonlinear conditions for the invariance of the solution set of an
equation under the group transformations by an equivalent linear
condition of infinitesimal invariance under the corresponding
infinitesimal generators of the group action.
My talk consists of two parts. Firstly, I will provide an (infinitesimal)
characterization of symmetries that is different from the standard one,
generalizing a similar characterization in the special settings of ODEs
and evolution equations to the setting of passive orthonomic systems.
And secondly, I will review some results on the symmetry-classification
of integrable evolution equations.
Popov Forms of Matrices of Differential Polynomials
George Labahn
D. R. Cheriton School of Computer Science,
University of Waterloo, Ontario, Canada
glabahn@cs.uwaterloo.ca
Popov normal forms were introduced by V. Popov for matrices of
polynomials in the middle 1960s as an alternative to the better known
Hermite normal form. They were found to have better properties for use
in the context of linear control theory. In this talk we will discuss
Popov normal forms for matrices of differential operators. We show
their usefulness in the context of systems of linear differential
equations and discuss the various computational challenges in
computing the forms for arbitrary matrices of differential operators.
Simplifying Skew Fractions Modulo Quasi-Linear Difference Relations
Ziming Li
Key Laboratory of Mathematics Mechanization,
AMSS,
Chinese Academy of Sciences, Beijing, China
zmli@mmrc.iss.ac.cn
This work is motivated by simplifying transfer functions (matrices)
of nonlinear discrete-time input/output systems in control theory.
Let 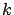 be a field of characteristic zero, and
be a field of characteristic zero, and 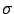 an
automorphism of
an
automorphism of 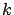 . Consider a first-order quasi-linear system
. Consider a first-order quasi-linear system
where
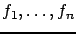 are rational functions. We present a
criterion that determines whether the field
is difference field with the induced
monomorphism
are rational functions. We present a
criterion that determines whether the field
is difference field with the induced
monomorphism
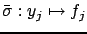 ,
,
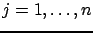 . We
construct its inversive closure
. We
construct its inversive closure 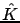 when
when 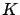 is a difference field.
is a difference field.
Let 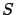 be the skew polynomial ring
be the skew polynomial ring
![$ \hat{K}[\partial;
\bar{\sigma}]$](img14.png) . We describe a few approaches to computing the
greatest common left divisors (gcld's) of two polynomials in
. We describe a few approaches to computing the
greatest common left divisors (gcld's) of two polynomials in 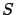 .
Every element in the left-fraction field of
.
Every element in the left-fraction field of 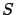 can be simplified by
removing the gcld of its numerator and denominator.
can be simplified by
removing the gcld of its numerator and denominator.
The transfer function for a discrete-time single-input single-output
equation is an element of the left-fraction field of 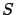 , while the
transfer matrix for a discrete-time multiple-input multiple-output
system has entries in the same skew-field. The goal of our
investigation is to develop efficient algorithms for manipulating
transfer functions (matrices).
, while the
transfer matrix for a discrete-time multiple-input multiple-output
system has entries in the same skew-field. The goal of our
investigation is to develop efficient algorithms for manipulating
transfer functions (matrices).
This talk is based on joint work with Martin Ondera, and Huaifu
Wang.
Discrete gradients
Elizabeth L. Mansfield and G. Reinout W. Quispel
and G. Reinout W. Quispel
 University of Kent, UK
University of Kent, UK
 La Trobe University, Australia
La Trobe University, Australia
E.L.Mansfield@kent.ac.uk
Discrete gradients approximate the flow of a gradient vector
field and have several important properties that make them
interesting to geometric integrators. In particular, when used
with a symplectic form to approximate a hamiltonian flow,
exact conservation of integrals may be obtained.
In this talk we discuss the definition and applications
of discrete gradients, and show how they relate to symbolically
determined function spaces defined in terms of moments.
In particular we show how
an infinite set of discrete gradients may be obtained, exactly in
a symbolic computation environment, for a given function.
The talk concludes with a discussion of on-going work and open
problems.
The authors wish to thank the Institute of Advanced Studies, LaTrobe
University and the Australian Research Council.
Invariant Variational Problems and Invariant Flows
Peter J. Olver
School of Mathematics,
University of Minnesota,
Minneapolis, USA
olver@umn.edu
I will present the moving frame approach to the analysis of invariant
variational problems and the evolution of differential invariants
under invariant submanifold flows. Applications will include
differential geometric flows, solitons and Poisson structures, and
computer vision.
Symbolic Analysis in Combinatorics and Special Functions
Peter Paule
Research Institute for Symbolic Computation,
Johannes Kepler University, Linz, Austria
ppaule@risc.uni-linz.ac.at
The talk presents a variety of applications of symbolic analysis:
orthogonal polynomials (e.g. positivity and log-concavity of coefficients),
special function inequalities, definite integrals from physics,
hypergeometric series, and combinatorial (multiple) sums.
In all these examples I illustrate the usage of computer algebra
software developed in my group at RISC.
Integro-Differential Polynomials and Boundary Problems
Markus Rosenkranz, Georg Regensburger
Radon Institute for Computational and Applied Mathematics,
Austrian Academy of Sciences, Linz
Markus.Rosenkranz@oeaw.ac.at
While differential polynomials can be used for formally adjoining
solutions of nonlinear ordinary differential equations (and systems),
their initial or boundary conditions are typically ignored. We
introduce a new algebraic structure that tries to remedy this flaw:
The integro-differential polynomials can be seen as a generalization
of differential polynomials that includes integral operators and the
corresponding evaluations. By incorporating the Baxter rule
(``integration by parts''), they also contain the shuffle algebra.
Our approach is constructive by using a suitable system of canonical
forms. The result is an integro-differential algebra: one can add,
multiply, differentiate, integrate, and evaluate integro-differential
polynomials. Formal solutions can be adjoined by factoring out the
(integro-)differential equation and its initial conditions.
Moving Frames for Laplace Invariants
Ekaterina Shemyakova
RISC, Hagenberg, Austria.
kath@risc.uni-linz.ac.at
The development of symbolic methods for the factorization and integration of
linear PDEs, many of the methods being generalizations of the Laplace
transformations method, requires the finding of complete generating sets of
invariants for the corresponding linear operators and their systems with
respect to the gauge transformations
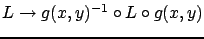 . Within the theory of Laplace-like methods, there is no uniform
approach to this problem, though some individual invariants for hyperbolic
bivariate operators, and complete generating sets of invariants for
second- and
third-order hyperbolic bivariate ones have been obtained.
. Within the theory of Laplace-like methods, there is no uniform
approach to this problem, though some individual invariants for hyperbolic
bivariate operators, and complete generating sets of invariants for
second- and
third-order hyperbolic bivariate ones have been obtained.
We show a systematic and much more efficient approach to the same
problem by application of moving-frame methods. We give explicit formulae for
complete generating sets of invariants for second- and third-order
bivariate linear operators, hyperbolic and non-hyperbolic, and also
demonstrate
the approach for pairs of operators appearing in Darboux transformations.
Differential Groups and the Gamma Function
Michael Singer
Department of Mathematics, North Carolina State Univerity, Raleigh, USA.
singer@math.ncsu.edu
I will present a Galois theory of linear difference equations
where the Galois group are linear differential groups that is, groups of
matrices whose entries satisfy a fixed set of polynomial differential
equations. These groups measure the differential dependence among
solutions of linear difference equations.
I will give a general introduction to the theory of linear differential
groups anddiscuss how this theory can be used to reprove Hölder's
Theorem that the Gamma function satisfies no differential polynomial
equation as well as new results concerning differential dependence of
solutions of higher order difference equations, such as families of
q-hypergeometric equations.
This is joint work with Charlotte Hardouin.
General differential Galois Theory
Hiroshi Umemura
Graduate School of Mathematics, Nagoya University, Japan
umemura@math.nagoya-u.ac.jp
General differential Galois theories are rapidely developping in
recent years. We talk about historical background and explain that our
theory is quite accesible, depending on a few simple principles.
We try to be as concrete as possible. We further present
applications of our theory to show how it is useful. We also discuss
open problems.
Investigating identities between Appell's
and univariate hypergeometric functions
Raimundas Vidunas
Kobe University, OAST, Japan
vidunas@math.kobe-u.ac.jp
Identities between bivariate and univariate hypergeometric
functions are desirable
in simplifying multiple sums or transformation to terminating
hypergeometric series.
In the talk we look for univariate specializations of
Appell's bivariate hypergeometric functions
that can be expressed in terms of univariate
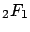 ,
, 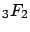 or
or 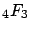 hypergeometric functions. The method is identifying cases when the
partial differential equations for Appell's functions imply hypergeometric
ordinary differential equations for their univariate specializations.
In general, ordinary differential equations for univariate specializations
of Appell's functions have order at most 4.
hypergeometric functions. The method is identifying cases when the
partial differential equations for Appell's functions imply hypergeometric
ordinary differential equations for their univariate specializations.
In general, ordinary differential equations for univariate specializations
of Appell's functions have order at most 4.
As this work produces interesting but not immediately complete
computations with a computer algebra package (like Maple or
Mathematica),
we try to formulate and demonstrate principles for electronic
"preprint" or "article" publication
of such computations,
to be usable and perhaps developable further by other researchers.
Computing Dimension of Solution Spaces for Linear Functional
Systems
Min Wu
Institute of Theoretical Computing, East China Normal University,
Shanghai, China
mwu@sei.ecnu.edu.cn
A linear (partial) functional system is a mathematical abstraction
of common properties of linear partial differential, difference
operators or any mixture thereof. In this talk, we present an
approach to determining dimension of solution spaces of linear
functional systems. We introduce the notion of reflexive modules,
which are naturally associated with reflexive systems that have the
same solutions as the original system. We show that linear dimension
of a linear functional system can be determined by Gröbner basis
computation of reflexive modules over Ore algebras.



Next: About this document ...
Evelyne Hubert
2008-05-26
![]() 'th order (
'th order (![]() ) right-hand
factors of a given linear difference operator with polynomial coefficients.
) right-hand
factors of a given linear difference operator with polynomial coefficients.
![]() be a field of characteristic zero, and
be a field of characteristic zero, and ![]() an
automorphism of
an
automorphism of ![]() . Consider a first-order quasi-linear system
. Consider a first-order quasi-linear system
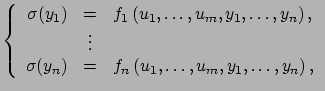
![]() be the skew polynomial ring
be the skew polynomial ring
![]() . We describe a few approaches to computing the
greatest common left divisors (gcld's) of two polynomials in
. We describe a few approaches to computing the
greatest common left divisors (gcld's) of two polynomials in ![]() .
Every element in the left-fraction field of
.
Every element in the left-fraction field of ![]() can be simplified by
removing the gcld of its numerator and denominator.
can be simplified by
removing the gcld of its numerator and denominator.
![]() , while the
transfer matrix for a discrete-time multiple-input multiple-output
system has entries in the same skew-field. The goal of our
investigation is to develop efficient algorithms for manipulating
transfer functions (matrices).
, while the
transfer matrix for a discrete-time multiple-input multiple-output
system has entries in the same skew-field. The goal of our
investigation is to develop efficient algorithms for manipulating
transfer functions (matrices).