


Next: Arithmetic
Up: User's Guide
Previous: User's Guide
Contents
Index
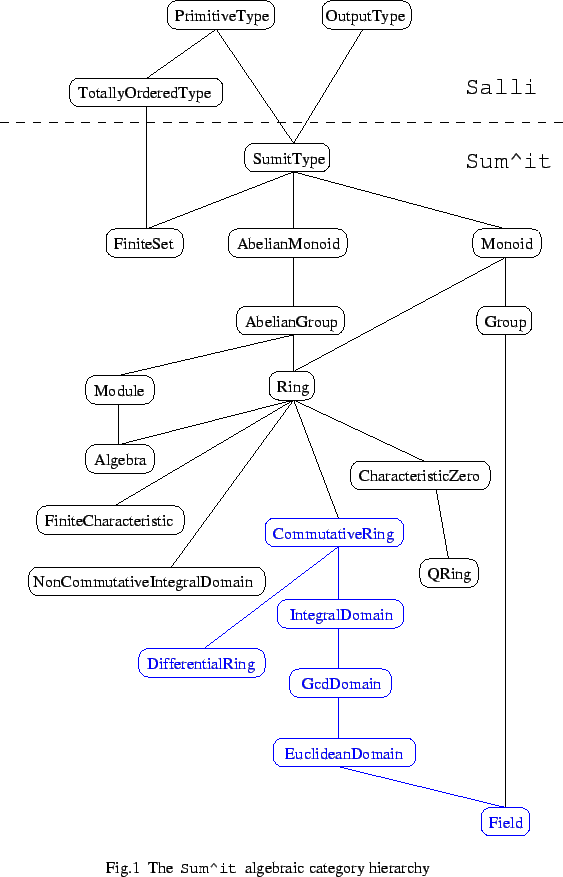
The basic algebraic categories provided by
 are shown in Figure 1.
While it follows quite closely the usual algebraic structures, a few
points needs to be mentioned.
are shown in Figure 1.
While it follows quite closely the usual algebraic structures, a few
points needs to be mentioned.
- The multiplication
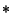 is in general not assumed to be commutative,
except in the subtree starting at CommutativeRing, which appears
in blue in Figure 1. This means that code written for the other categories
should be careful and not assume commutativity of
is in general not assumed to be commutative,
except in the subtree starting at CommutativeRing, which appears
in blue in Figure 1. This means that code written for the other categories
should be careful and not assume commutativity of 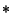 . Addition is on
the other hand always assumed commutative.
. Addition is on
the other hand always assumed commutative.
- The
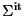 category tree has a unique root SumitType to which
almost all the types provided by
category tree has a unique root SumitType to which
almost all the types provided by
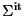 belong. The category
SumitType inherits PrimitiveType from SALLI,
which means that types in
belong. The category
SumitType inherits PrimitiveType from SALLI,
which means that types in
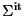 must export an equality.
That equality however does not need to be complete, as described
in the
must export an equality.
That equality however does not need to be complete, as described
in the  page of the SALLI reference manual.
SumitType plays also an important role in input/output as
explained below.
page of the SALLI reference manual.
SumitType plays also an important role in input/output as
explained below.
- The SALLI categories ArithmeticType and AdditiveType
already export the basic arithmetic operations provided respectively
by rings and abelian groups, and in fact Ring and
AbelianGroup do inherit from them. There is however
a fundamental difference: while ArithmeticType and
AdditiveType export the usual operations
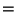 ,
, 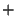 ,
,  ,
,
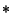 ,..., they make no assumption about their algebraic properties
whatsoever. On the other hand, the corresponding algebraic categories
in
,..., they make no assumption about their algebraic properties
whatsoever. On the other hand, the corresponding algebraic categories
in
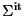 do assume that
do assume that 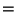 is a complete equality test, and that
the arithmetic operations satisfy the algebraic axioms of their
mathematical structure. So for example, while Integer is
extended by
is a complete equality test, and that
the arithmetic operations satisfy the algebraic axioms of their
mathematical structure. So for example, while Integer is
extended by
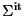 to be a Ring (among other things),
SingleFloat remains an ArithmeticType but is
not a Ring. There are similar correspondances between
LinearCombinationType and Module, and between
LinearArithmeticType and Algebra.
Mathematical types such as
DenseMatrix
to be a Ring (among other things),
SingleFloat remains an ArithmeticType but is
not a Ring. There are similar correspondances between
LinearCombinationType and Module, and between
LinearArithmeticType and Algebra.
Mathematical types such as
DenseMatrix or
DenseUnivariatePolynomial
or
DenseUnivariatePolynomial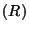 allow their argument
allow their argument 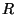 to be an ArithmeticType rather
than a Ring, but those among their functions that require
a complete equality on
to be an ArithmeticType rather
than a Ring, but those among their functions that require
a complete equality on 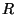 are not exported when
are not exported when 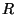 is not a Ring.
Similarly, while DenseUnivariatePolynomial
is not a Ring.
Similarly, while DenseUnivariatePolynomial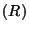 is always an
ArithmeticType, it is a Ring only when
is always an
ArithmeticType, it is a Ring only when  itself
is a Ring. For example,
itself
is a Ring. For example,
is a valid type in
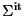 , but Gaussian elimination is not available for
such matrices, and the Euclidean algorithm is not available for their
polynomial entries. Basic arithmetic, as provided by ArithmeticType
is however available.
, but Gaussian elimination is not available for
such matrices, and the Euclidean algorithm is not available for their
polynomial entries. Basic arithmetic, as provided by ArithmeticType
is however available.




Next: Arithmetic
Up: User's Guide
Previous: User's Guide
Contents
Index
Manuel Bronstein
2000-12-13