Health-e-Child - IST-2004-027749 - Deliverable D.11.4

Brain Tumours

Tumour Growth Modelling in the Brain

5. Identifying Model Parameters

In cancer treatment, understanding the aggressiveness of the tumour is essential in therapy planning and patient follow-up. In this work we propose a method for quantifying the progression of the critical target volume (CTV) of glial-based tumours, on the basis of their growth dynamics. The formulation is based on the tumour growth model proposed by [Clatz et al., 2005], which uses reaction-diffusion formalism:

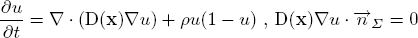
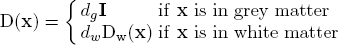
With the proposed method, we obtain quantitative estimates for the speed of invasion in white and grey matter by solving the patient specific parameter identification problem for this growth model using MR images taken at two different time instances, t₁ and t₂, from the same patient. The parameter identification problem is formulated using the front approximation of reaction-diffusion equations, which results in anisotropic Eikonal equations. The anisotropic fast marching method proposed in [Konukoglu et al., 2007a] is used for numerical solutions yielding an efficient algorithm.

5.1 Method

The model given above requires tumour cell density u to be known at every point as an initial condition. However, this is not the case for medical images where only contours around gross tumour volume (GTV) and CTV are available. The front motion approximation of reaction-diffusion equations offers a solution for this discrepancy between information needed and observations available [Konukoglu et al., 2007b]. Taking the contour around the CTV, Γ, as the last visible tumour front we can use such an approximation to model its evolution. As a result we obtain the following travelling wave formulation:

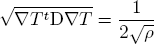
where T(x) represents the time at which Γ passes from point x.

In order to formulate the inverse problem we follow the modelling assumption as given in [Clatz et al., 2005] and state T(Γ₁)=0 and T(Γ₂)=t₂-t₁, where Γ₁ and Γ₂ corresponds to contours around CTV regions observed in images taken at time t₁ and t₂ respectively. Parameter identification process tries to find parameters d_g and d_w that create a T function that would satisfy these conditions. Notice that ρ is a multiplicative factor in the travelling time formulation and it cannot be determined independently from the D matrix by just looking at the motion of the tumour front. To tackle this, we treat ρ as a known constant in the parameter identification problem. t₁ is not available in clinical circumstances hence we use t₂-t₁. The formulation can be given as the minimisation problem

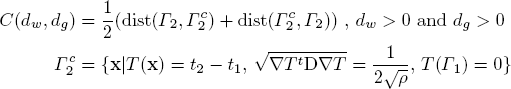
where C is the objective function to minimise with respect to d_w and d_g, Γ₂^c is the computed contour using the front approximation with the given parameters and dist(A,B) is the distance between two iso-surfaces taken as mean distance from voxels of A to the closest voxel of B.

Left: T2 weighted MR images of a patient taken at t₁ and t₂ and the tumour delineations around the tumour infiltrated oedema Γ₁ and Γ₂ manually done. Right: The minimisation surface C(d_w, d_g) for the parameter identification problem given by the images on the left.

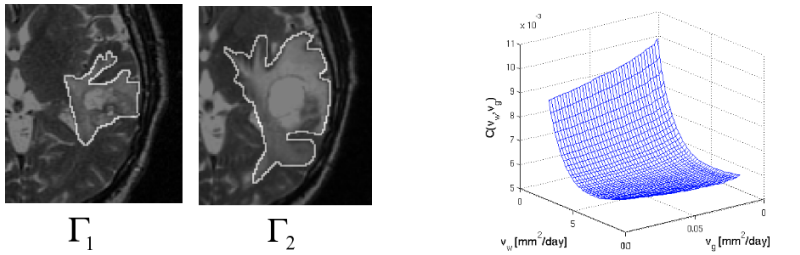
5.2 Minimising Parameters

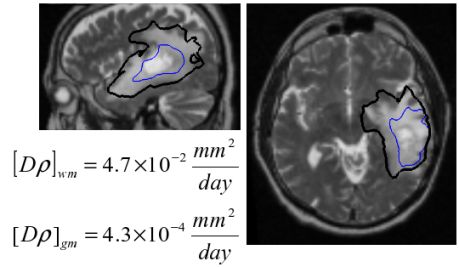
The method explained in the previous section allows us to identify the diffusion related parameters of the reaction-diffusion based growth model. In identifying these parameters we solve the quantification problem: How fast is the tumour growing? The way we answer this question is by providing two parameters corresponding to speed of diffusion of tumour cells in the grey matter and in the white matter. Such an approach quantifies the spiky nature of invasion of brain tumours, which can be very hard to capture using methods such as measuring the diameter of the tumour. Although we demonstrate the method on high grade gliomas, same idea extends to low grade gliomas which are modelled using similar formulations.

Sagittal and axial slices of a patient suffering from a high grade glioma is given. The underlying image is taken at t₂. Blue contours: The tumour delineation at t₁ manually done by an expert, Γ₁. Black contours: The tumour front computed by the travelling time formulation Γ₂* with the parameters minimising the functional d_w* and d_g*. The minimising speed values in the grey and in the white matter are also given in the image. Observe how the computed black contour is close to the CTV in the underlying image. Observe the very high difference between white matter and grey matter speed which is coherent with the experimental observations.

5.3 References

• [Clatz et al., 2005] Clatz, O., Sermesant, M., Bondiau, P., Delingette, H., Warfield, S. Malandain, G., Ayache, N., 2005. Realistic simulation of the 3d growth of brain tumors in mr images coupling diffusion with biomechanical deformation. IEEE TMI, 24.
• [Konukoglu et al., 2007a] Konukoglu, E., Sermesant, M., Clatz, O., Peyrat, JM, Delingette, H., Ayache, N., 2007. A recursive anisotropic fast marching approach to reaction diffusion equation: application to tumor growth modeling., IPMI 2007.
• [Konukoglu et al., 2007b] Konukoglu, E., Clatz, O., Bondiau, P., Sermesant, M., Delingette, H., Ayache, N., 2007. Towards an Identification of tumor growth parameters from time series of images, to be presented at Miccai 2007.