Health-e-Child - IST-2004-027749 - Deliverable D.11.4

Brain Tumours

Tumour Growth Modelling in the Brain

1. Literature review and general overview

1.1 Introduction

Tumour growth modelling is the study of complex dynamics of cancer progression using mathematical descriptions. Internal dynamics of cancerous cells, their interactions with each other and with healthy tissue, nutrition and oxygen transport from the extracellular matrix (ECM) and from the vascular network, chemicals secreted by tumour cells, type of the underlying tissue and many other factors are modelled by mathematical abstractions. These abstractions rely on biological and clinical observations coming from different sources at different scales. Example observations include in-vitro experiments, in-vivo experiments on animal subjects, biopsy and autopsies results, medical images of patients like computed tomography (CT) scans or magnetic resonance images (MRIs). These experimental results and images are keys to develop models describing the tumour growth process accurately.

Mathematical growth models offer important tools for both clinical and research communities in oncology. By providing a common mathematical ground to combine experimental findings made in many diverse fields of cancer research they allow us to interpret such experimental results and understand the underlying mechanisms of tumour growth. Virtual experiments and simulations give the opportunity to observe effects of different treatments on cancerous cells, and could lead to improve these treatments or suggest new ones. Personalised models, adapted to patient specific cases, could be used in therapy planning by suggesting irradiation regions adapted to growth dynamics or optimal temporal distribution of chemotherapy.

1.2 Mathematical Growth Models

Tumour growth modelling has received considerable attention in the literature and there has been a vast amount of work during the last 15 years. A complete review of all the work done on this subject is outside the scope of this page. Here, we synthesise the main approaches towards this problem and review some of the latest work, in view of giving the reader an overview of the current trends.

Tumour growth is an extremely complicated process consisting of different interacting sub-processes at different scales. Proposed models concentrate on one or several of these sub-processes. Research conducted on tumour growth modelling can be coarsely classified into two large groups: microscopic models and macroscopic models. The main difference between these two classes is the scale of observations they are trying to explain and formulate. Microscopic models concentrate on observations in the microscopic scale, like in-vitro and in-vivo experiments. As a result they formulate the growth phenomena at this scale. Macroscopic models on the other hand, concentrate on observations at the macroscopic scale like the ones provided by medical images. They formulate the average behaviour of tumour cells and their interactions with underlying tissue structures, which are visible at this scale of observation (grey matter, white matter, bones...). These models try to describe the behaviour of the tumour as a whole, consisting of millions of cells.

Further classification within these groups can be made based on the stage of the tumour growth being analysed (avascular growth, angiogenesis and vascular growth) or the effect of the growth on the brain (diffusion/invasion of tumour cells and mass-effect). In this review we use the classification based on the stage for the microscopic models and the one based on the effect for the macroscopic models for better comprehension.

Classification of tumour growth models: First level classification is based on the scale of the model and scale of the observation model uses. Second level classification is based on the stage of the tumour growth for microscopic models and effect of the tumour for the macroscopic models.

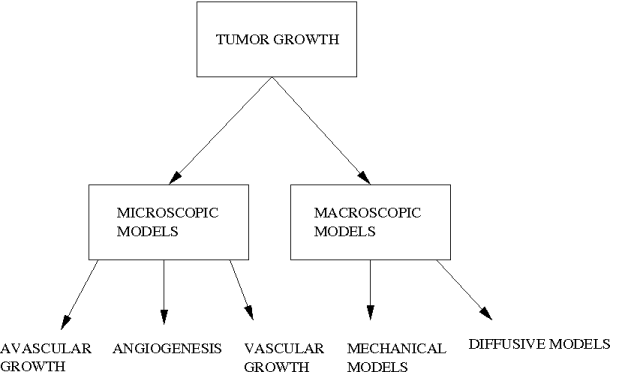
1.2.1 Microscopic Models

Microscopic growth models aim to describe the tumour growth process at the cellular level based on the experimental observations at this level. They take into account physical and chemical interactions between cancer cells, the extra-cellular matrix and the healthy cells. Mechanical phenomenon like pressure, cohesion and adhesion forces are often included in these descriptions. As for chemical interactions, microscopic models formulate phenomena like diffusion of nutrition and oxygen, secretion of different factors by tumour cells and their effects on the surrounding. Mathematical systems obtained for these models are usually very detailed because they try to take into account all the observed factors. As a consequence, the number of parameters for such models are very high. From the technical point of view, formulations used in microscopic models enjoy a large variety of mathematical methods. Most commonly used methods are partial differential equation (PDE) systems, cellular automata and statistical models.

• Avascular Growth/Solid Tumour:

The avascular growth corresponds to the stage where the growth process is mostly governed by the proliferation of tumour cells. In this stage the tumour is considered to be a solid mass, which is growing by mitosis. Although not completely known, it is thought that there is no invasion of the healthy tissue. The interactions between tumour cells and the healthy tissue is also thought to be limited [Araujo and McElwain, 2004]. The tumour cannot grow indefinitely in the avascular stage because as the tumour mass grows, less and less nutrition is available for the cells deep inside the avascular mass. As a result, necrosis begins: tumour cells that are not getting enough nutrition die, and only cells on the outer perimeter of the tumour continue to proliferate. At one point necrosis and the proliferation balances each other and the avascular tumour reaches a limit size, which is assumed to be around 1-3 mm in diameter [Orme and Chaplain, 1996].

Most growth models proposed to formulate this stage try to describe mathematically three different experimental observations: the formation of the necrotic core, dormancy of the tumour at the limit size and the motion of cancerous cells within the solid tumour. In order to achieve this, they formulate different causes like:

• Mitosis/Population growth,
• Distribution and consumption of oxygen,
• Apoptosis/Programmed cell death,
• Surface tension,
• Cell cycles,
• Secretion and diffusion of growth inhibitory hormones (GIFs),
• Chemotaxis/Active migration,
• ...
Building blocks of these models are coupled ordinary and partial differential equations such as population growth and reaction-diffusion. Variation of parameters of these equations have also been studied to assess the importance of deviation from the mean behaviour.

• Tumour-Induced Angiogenesis:

This is the stage where tumour cells in the avascular mass modify the existing vascular structure to create new vessels that would feed them. Through this process the tumour can overcome its limit size, grow much faster and invade the surrounding tissue. Due to this crucial role of angiogenesis, the underlying mechanisms of this stage have captured attention and many models have been proposed.

Tumour-induced angiogenesis is a very complex process including lots of chemical and mechanical phenomenon, which have not been totally understood. [Mantzaris et al., 2004] reviewed some of the known biological processes taking place in angiogenesis. The basic observable consequence is that tumour cells affect nearby blood vessels to sprout new vessels towards itself, creating new vascular structure. As a result of angiogenesis, the tumour receives extra nutrients and oxygen and the growth speeds up. Mathematical formulations of this stage usually takes into account the motion of endothelial cells (ECs), tumour angiogenesis factor (TAF), fibronectin structures of extracellular matrix (ECM), vascular endothelial growth factor (VEGF) and angiogenesis inhibitor factors.

As in the case of solid tumour growth, many angiogenesis models are based on integro-differential equations. In most of them the diffusion of the above-mentioned chemicals and the density of blood vessels are formulated using reaction-diffusion equations. In addition to these, some discrete models are trying to predict the structure of the formed vasculature in 2D, rather than formulating it as a density. Such discrete models use different tools like Nash games and stochastic differential equations.

• Vascular Growth/ Invasive Tumour:

The third stage of the tumour growth, vascular growth, has been paid less attention than the two previous stages. The complexity of the tumour growth in this stage is higher because there are several processes going on simultaneously. In addition to cellular and chemical interactions going on as in first two stages, tumour cells start to invade the surrounding tissue via mechanisms that are not clearly known yet. At this stage, the tumour becomes diffusive and is not considered to be solid anymore. While the difference between cancerous and healthy regions are clear in the avascular stage, this difference vanishes during the vascular growth because tumour cells move towards healthy regions. Vessels inside the vascular tumour might have been formed by angiogenesis or the tumour might have initialised around a vessel, as in the case of tumour cords. Unlike avascular tumours, the source of nutrition is not limited to diffusion from the perimeter. Thus, the formation of necrotic regions is much more complex, if they exist at all. For the same reasons, vascular tumours are not compact masses of cancerous cells, they don't have a limit size and they can grow indefinitely.

First models examining the vascular invasion concentrated on the metastases process (invasion through blood stream). Using similar ideas, the local invasion is modelled by formulating the infiltration of the tumour cells. Different models have taken different approaches for this. Some groups modelled the infiltration as directed diffusion, particularly towards blood vessels, or as an active transport, resulting in a reaction-diffusion formalism. At the opposite of these continuum models, some cellular automata models were also proposed for the dynamics of cancerous cells, along with a reaction-diffusion formalism for the chemicals taking a role in the growth process. Besides the methodological differences with the previous models, new phenomena like the effect of the acidic metabolism of tumour cells or the effect of the vascular structure on the tumour growth are studied and included in vascular/invasion models.

1.2.2 Macroscopic Models

Observations at the macroscopic scale consists of medical images like computed tomography scans (CT), magnetic resonance images (MRI) and MR diffusion tensor images (MR-DTI). Since the resolution of these observations is limited, typically around 1mm x 1mm x 1mm in the best case, observable factors are limited. Mathematical models at the macro-scale try to formulate the tumour growth using observations coming from this scale. For this reason, these models include fewer factors and are mathematically simpler than the microscopic models of Section 1.2.1. On the other hand, while microscopic models simulate the tumour growth in theoretical settings (infinite boundaries, known location of different structures,...), macroscopic models use real settings personalised for each patient , e.g. real boundaries of the brain, grey-white matter segmentation...

Based on the effect of the tumour on the brain, macroscopic models can be classified in two different classes: mechanical models, which concentrate on the mass-effect of the tumour on the brain tissue, and diffusive models, which concentrates on the invasion of surrounding tissue by tumour cells. From the mathematical point of view, all macroscopic models use continuum formulations based on a continuous local density or proportion of tumour cells. As a result, formulations contain several ordinary and/or partial differential equations to describe the growth process.

• Diffusive Models:

Almost all diffusive macroscopic models use the reaction-diffusion formalism. This formalism models the invasive tumour by adding a diffusion term to simple solid tumour growth models, which formulates proliferation of cells, see table 1. The "building block" equation of this formalism is the partial differential equation (PDE) given as:



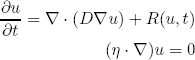
where u is the tumour cell density, D is the diffusion tensor of tumour cells and R(u,t) is the so-called reaction term. This equation isolates two different characteristics of the tumour growth in the two terms: diffusion and proliferation. The first term on the right hand side describes the invasion of tumour cells by means of a directed Brownian motion, which is characterised by the diffusion tensor D. The second term in the equation, R(u,t), describes the proliferation of tumour cells. The second equation represents the no-flux boundary condition which is applied at the skull and ventricles, formulating the fact that tumour cells do not diffuse towards these structures.

Recent works on diffusive models concentrates on the infiltration part of the equation, in other words on the diffusion tensor. Following the experimental results showing the high infiltration speed of tumour cells on the myelin sheath, several models proposed to use an isotropic but heterogeneous D varying depending on the tissue (grey-white). Latest works also included the hypothesis that tumour cells actually follow the fibre tracts by creating an anisotropic tensor D.

• Mechanical Models:

Mechanical models, which concentrated on the mass-effect of the tumour, contain two distinct coupled formulations, one for the tumour growth and one for the mechanical characteristics of the brain tissue. These model tumour growth using rather a simpler formulation consisting only of mitosis (population growth model) causing an outwards pressure. They concentrate on the mechanical interaction between a growing tumour and the brain tissue whose characteristics are modelled with detail. There have been many works on characterising the mechanical properties of the brain tissue, which is deformable but not elastic.

In [Wasserman and Acharya, 1996] it is said that the brain tissue is a sponge like material, possessing instantaneous properties of elastic materials and time-dependent properties of the viscoelastic ones. Moreover, there is a great variation between elastic parameters of brain tissue within similar tissues as well as between differing tissues. Instead of formulating these complex mechanical characteristics, almost all models use assumptions to simplify brain tissue's characteristics. First works used linear elastic material properties for the brain tissue simplifying the model. However, this assumption did not allow large deformations usually observed in clinical cases. More recent works relaxed this assumption and used hyper elastic material properties obtaining these large deformations.

On the other hand, some recent works kept the linear elastic material assumption but tried to improve the tumour growth model. Eventually they obtained a coupling between more complicated diffusive models explained above and a simpler mechanical model describing the deformation of the brain tissue.

1.3 References

• [Araujo and McElwain, 2004] Araujo, R. and McElwain, D., 2004. A history of the study of solid tumor growth: the contribution of mathematical modeling. Bul. Math. Biology, 66.
• [Mantzaris et al., 2004] Mantzaris, N., Webb, S., and Othmer, H., 2004. Mathematical modeling of tumor-induced angiogenesis. Journal of Math. Biology, 49.
• [Orme and Chaplain, 1996] Orme, M. and Chaplain M.A.J., 1996. A mathematical model of vascular tumor growth and invasion. Math. Comp. Modelling, 23.
• [Wasserman and Acharya, 1996] Wasserman, R. and Acharya, R., 1996. A patient-specific in-vivo tumor model. Math. Biosci.,136.
• Zheng, X., Wise, S., and Cristini, V., 2005. Nonlinear simulation of tumor necrosis, neo-vascularization and tissue invasion via an adaptive finite-element/level-set method. Bull. Math. Biology, 67.