Health-e-Child - IST-2004-027749 - Deliverable D.11.4

Brain Tumours

Computational Anatomy of the Brain

6. Example use of Computational Anatomic Models in the Clinical Workflow

6.1 Better Constrain Atlas-to-Patient Registration for Radiotherapy

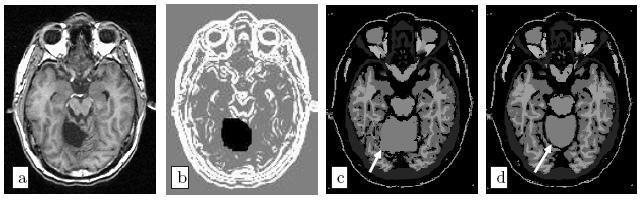
The planning step for conformal radiotherapy requires the accurate localisation of the tumour, to maximise its irradiation, and of the critical structures where the irradiation has to be minimises. To segment these structures for each patient, one standard method is to register a previously labelled atlas to the patient image. This allows transferring the generic atlas segmentation toward the patient-specific space. This segmentation can then be used directly, or as an initialisation for a more complex segmentation algorithm [Commowick, 2007]. In such a system, the main difficulty is to obtain an inter-subject registration algorithm which is accurate enough and, more importantly, robust to the anatomical variability and to the pathologies (tumours may be quite important).

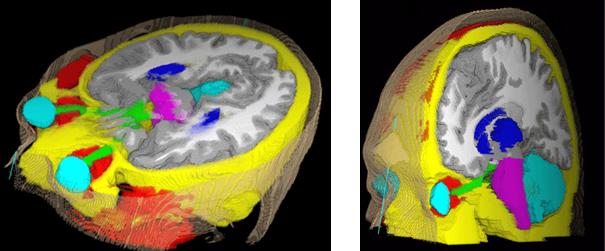
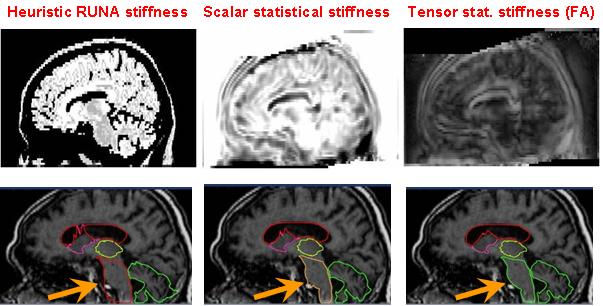
Figure 7. Structures of interest for conformal radiotherapy segmented by P.Y. Bondiau at CAL, Nice based on the MNI brain atlas [Bondiau, 2004].

The main method to enforce meaningful deformations is to penalise non sensible ones through a regularisation criterion. Some authors used physical models like elasticity or fluid models [Bajcsy and Kovacic, 1989, Christensen et al., 1997]. For efficiency reasons, other authors proposed to use non-physical but fast regularisation methods like Gaussian filtering [Thirion, 1998, Pennec et al., 1999, Modersitzki, 2004]. However, since we do not have in general a model of the deformation of organs across subjects, no regularisation criterion is obviously more justified than the others. Thus, most of the existing work in the literature rather tries to capture the organ variability from a statistical point of view on a representative population of subjects (see e.g. [Thompson et al., 2000, Rueckert et al., 2003, Fillard et al., 2005]). For instance, following [Lester et al., 1999], the algorithm RUNA developed in [Stefanescu et al., 2004, Stefanescu, 2005] was a first attempt to obtain a computationally efficient but highly steerable nonlinear registration algorithm that includes some anatomical information about the tissue types. It uses a non-stationary transformation regularisation which is strong where the local deformability is expected to be low, and conversely. This also allows taking into account pathologies such as tumours or previous resections.

Figure 8. Registration of the atlas towards the patient image to segment structures at risk for radiotherapy planning. a) Patient image, b) Stiffness field, c) Atlas deformed towards the patient images without taking into account the resection, d) Atlas deformed towards the patient images with the pathology taking into account.

Moreover, the regularisation can be locally tuned along spatial directions through the use of a tensor field, as we did for instance in [Commowick et al., 2005], by introducing a method to compute scalar and tensor based deformability statistics over a database of patient.

Figure 9. Comparative results of the atlas-based segmentation using RUNA guided by the heuristic scalar stiffness map (left), the scalar statistical stiffness map (middle) and the statistical tensor stiffness map (right). Top: image of the stiffness map used. Bottom: Sagittal slice of the 3D patient image with the segmentation superimposed. The inclusion of the statistical information clearly allows to better deform the brain stem area in an anatomically more meaningful way, resulting in a better and smoother segmentation. Brain images are courtesy of Dr. P.-Y. Bondiau, CAL, Nice.

6.2 Mapping the fibres to patient images for tumour growth models

As shown in the tumour growth model section, the DTI information is crucial in the formulation of the tumour growth model because tumour cells move much faster on the white matter and they tend to follow the fibre tracts. Hence, the infiltration pattern of the tumour highly depends on the local fibre directions. Since diffusion tensor images give the average local fibre orientation they can be used to extract these tumour highways as it was done in the model we have explained to construct the diffusion tensor of tumour cells. Unfortunately, DT-MRI images are seldom acquired in the clinical routine because of technical constraints (old clinical MR scanners often do not have gradients powerful enough to acquire this sequence), time constraints which are crucial for the image quality, especially on children (a typical DTI acquisition lasts about 10 minutes during which the child should not move, which may require sedation), ethical issues and economical efficiency (there is no clinical indication for DTI yet).

Thus, in order to use local fibre directions information for patients without DTI, we have to rely on a generic atlas of fibres, i.e. register tensors from a healthy subject onto the patient anatomy.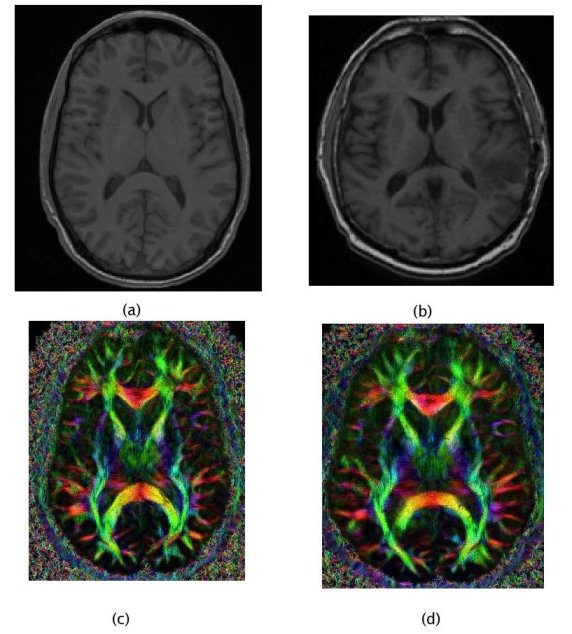

Example mapping of tensors from a healthy subject to a patient. (a) T1 weighted image of the healthy subject (atlas). (b) T1 weighted image of the patient. (c) DTI of the healthy subject in the standard colour mode. The colour encodes the principal direction of the tensor (green: front/back, red: left/right, blue: top/down), while the intensity is related to the fractional anisotropy which quantifies the reliability of this principal direction. (d) Result of the resampling of image (c) using the non-linear transformation found by the registration of the anatomical images (a) and (b).

In such a personalisation process, the quality of the registration algorithm is essential as it directly affects the model and the growth simulation. Thus, using prior knowledge about the inter-subject variability is necessary to obtain a fibre mapping which is anatomically meaningful. Once again, computational anatomy appears as a key component of the clinical image analysis work-flow.

6.3 References