This pages details the error calculation process, between the known sources and the ones that are computed by Fs3d.

Pairing

Given two sets of sources (source = {position, moment}), the first step to be taken consists in matching the sources of both sets. This section details the algorithm performing this operation.

Because the number of sources is small, all permutations are calculated and a cost is determined for each permutation.

For a given matching, the cost is obtained by summing the distances between sources. This is the criterion used to compare matching.

To build a known sources/estimated sources matching, the process uses backtracking. A source is selected in the first set, a second source is selected in the second set, and the partial cost is computed. This process is applied recursively until both sets are empty, or until the partial cost goes above the best already computed cost.

At the end, the matching is given by the permutation achieving the lowest overall cost.

Errors on position

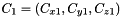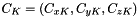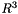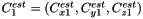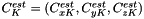In the following let $C_1=(C_{x1},C_{y1},C_{z1})$ to $C_K=(C_{xK},C_{yK},C_{zK})$ be the actual (known) sources positions (vectors in $R^3$ ), matched in this order to the estimated sources positions $C^{est}_1=(C^{est}_{x1},C^{est}_{y1},C^{est}_{z1})$ to $C^{est}_K=(C^{est}_{xK},C^{est}_{yK},C^{est}_{zK})$ .

For this matching several errors are computed:

a relative error vector given for each source numbered 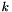( 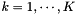$k= 1, \cdots, K$ ) by
$\frac{C_k-C^{est}_k}{\left|C_k\right|}=\frac{(C_{xk}-C^{est}_{xk},C_{yk}-C^{est}_{yk},C_{zk}-C^{est}_{zk})}{\sqrt{C_{xk}^2+C_{yk}^2+C_{zk}^2}}$
written as:
pair.first->position()-pair.second->position()/pair.first->position().length()
the associated error term, given by the modulus of the above vector:
$e_k=\frac{\left|C_k-C^{est}_k\right|}{\left|C_k\right|}=\sqrt{\frac{(C_{xk}-C^{est}_{xk})^2+(C_{yk}-C^{est}_{yk})^2+(C_{zk}-C^{est}_{zk})^2}{C_{xk}^2+C_{yk}^2+C_{zk}^2}}$
written as:
pair.first->position().length()
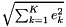
the global error, defined by the quadratic norm of the above quantities: $\sqrt{\sum_{k=1}^K e_k^2}$

Errors on moments

Errors between moments are more complicated to compute, because two moments are equivalent if they differ only by a real multiplicative coefficient 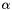$\alpha$ (normalisation). A preprocessing step is thus added for computing the value of this coefficient which we describe below.

With one source

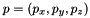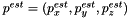Let $p=(p_{x},p_{y},p_{z})$ and $p^{est}=(p^{est}_{x},p^{est}_{y},p^{est}_{z})$ be respectively its actual and estimated moments. The 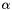$\alpha$ is defined as the value minimizing the following quantity:

$|p -\alpha p^{est}|^2= (p_{x}- \alpha p^{est}_{x})^2+(p_{y}- \alpha p^{est}_{y})^2+(p_{z}- \alpha p^{est}_{z})^2$

which is a polynomial expression in the unknown 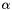$\alpha$ .

Let 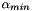$\alpha_{min}$ be the best possible 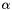$\alpha$ . Because the derivative of the above polynomial w.r.t. 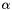$\alpha$ vanishes at 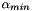$\alpha_{min}$ , it holds that:

$\alpha_{min} = \frac{p_{x}p^{est}_{x} + p_{y}p^{est}_{y} + p_{z}p^{est}_{z}}{(p^{est}_{x})^2 + (p^{est}_{y})^2 + (p^{est}_{z})^2} = \frac{p \cdot p^{est}}{|p^{est}|^2}$

With several sources

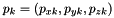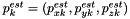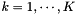With several sources of actual and estimated moments $p_k=(p_{xk},p_{yk},p_{zk})$ and $p^{est}_k=(p^{est}_{xk},p^{est}_{yk},p^{est}_{zk})$ for $k= 1, \cdots, K$ , the above computation is generalized as follows. We look now for 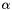$\alpha$ as the value minimizing the quantity (sum of the squared distance between vectors):

$\sum_{k=1}^K |p_k -\alpha p_k^{est}|^2 = \sum_{k=1}^K{\left[(p_{xk}- \alpha p^{est}_{xk})^2+(p_{yk}- \alpha p^{est}_{yk})^2+(p_{zk}- \alpha p^{est}_{zk})^2\right]}$

which is still a polynomial expression in 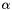$\alpha$ . The above expression for 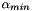$\alpha_{min}$ then becomes:

$\alpha_{min} = \frac{\sum_{k=1}^K{p_{xk}p^{est}_{xk} + p_{yk}p^{est}_{yk} + p_{zk}p^{est}_{zk}}}{\sum_{k=1}^K{\left[(p^{est}_{xk})^2 + (p^{est}_{yk})^2 + (p^{est}_{zk})^2\right]}} = \frac{\sum_{k=1}^K{p_k \cdot p^{est}_k}}{\sum_{k=1}^K{|p^{est}_k|^2}}$

which is implemented as:

double dotProduct=0, length=0, alpha;
for(QPair<fs3dDipoleData*,fs3dDipoleData*> pair:d->bestMapping)
{
    dotProduct+=QVector3D::dotProduct(pair.first->moment(),pair.second->moment());
    length+=pair.second->moment().lengthSquared();
}
alpha=dotProduct/length;

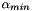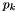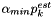Once $\alpha_{min}$ is determined, the matching between $p_k$ and $\alpha_{min} p^{est}_k$ and the global error on moments are computed as for the source positions (see above).